[Internal] Các thuật toán thông dụng trong lắp ráp bộ gen
Writer: @Anh Vu Mai Nguyen
Advisors: @Khai Tran @Thanh Nguyen
Nghiên cứu và phát triển thuật toán không chỉ để cho học sinh, sinh viên, lập trình viên mang đi tham gia các cuộc thi như Olympic Tin học Quốc tế, ACM-ICPC hay thi đấu với nhau trên các trang LeetCode, HackerRank, SPOJ, TopCoder, CodeForces hay CodeChef. Các thuật toán này còn được ứng dụng vào trong các ngành công nghiệp, các sản phẩm công nghệ thông tin và các ngành khoa học nghiên cứu khác chẳng hạn thuật toán CHIRP dựng hình ảnh hố đen đầu tiên. Các thuật toán hỗ trợ con người giải được các bài toán trong nhiều lĩnh vực khác nhau nhanh hơn, chính xác hơn, góp phần làm cho cuộc sống tốt hơn. Trong lĩnh vực y sinh, thuật toán ngày càng đóng vai trò quan trọng hơn khi khối lượng dữ liệu về y sinh đang bùng nổ liên tục theo thời gian. Bài viết này sẽ cắt một lát nhỏ thuật toán trong lĩnh vực tin sinh chuyên dùng để lắp ráp bộ gen đã và đang được dùng trên thế giới.
Tại sao cần thuật toán để lắp ráp bộ gen?
Gen là một khái niệm thay đổi qua từng thời kì. Tuy nhiên, để đơn giản hóa, trong bày viết này khi nhắc đến gen chúng ta hiểu gen là tổ hợp các kí tự (base) A, T, G, C một cách không ngẫu nhiên, tạo thành những mô-típ nhất định, những đoạn lặp ngắn, dài. Theo Genome Reference Consortium, bộ gen con người là một chuỗi dài 3 tỉ kí tự như vậy.
Tuy sự phát triển của công nghệ giải trình tự gen đã có những tiến bộ vượt bậc so giúp giảm chi phí rất nhiều từ hơn 100.000.000$ về khoảng 1.000$, con người vẫn chưa thể “lôi” được một chuỗi DNA siêu dài ra và đọc toàn bộ, chúng ta buộc phải cắt nhỏ bộ gen ra và đọc từng phần một, sau đó lắp ráp chúng lại với nhau. Nếu chỉ lấy sợi DNA từ một tế bào, thì tín hiệu thu được quá thấp, nên thực tế chúng ta lại phải lấy từ nhiều tế bào khác nhau, cắt nhỏ, rồi mới đọc. Từ thực nghiệm và chứng minh bằng thống kê cho thấy, với phương pháp đọc từng đoạn ngắn của gen dài 150 kí tự, mỗi điểm trên bộ gen cần được bao phủ trung bình 30 lần mới đảm bảo độ chính xác. Lúc này, lượng kí tự lưu trữ cho mỗi bộ gen người đã không còn là 3 tỉ kí tự nữa, mà là 90 tỉ kí tự.
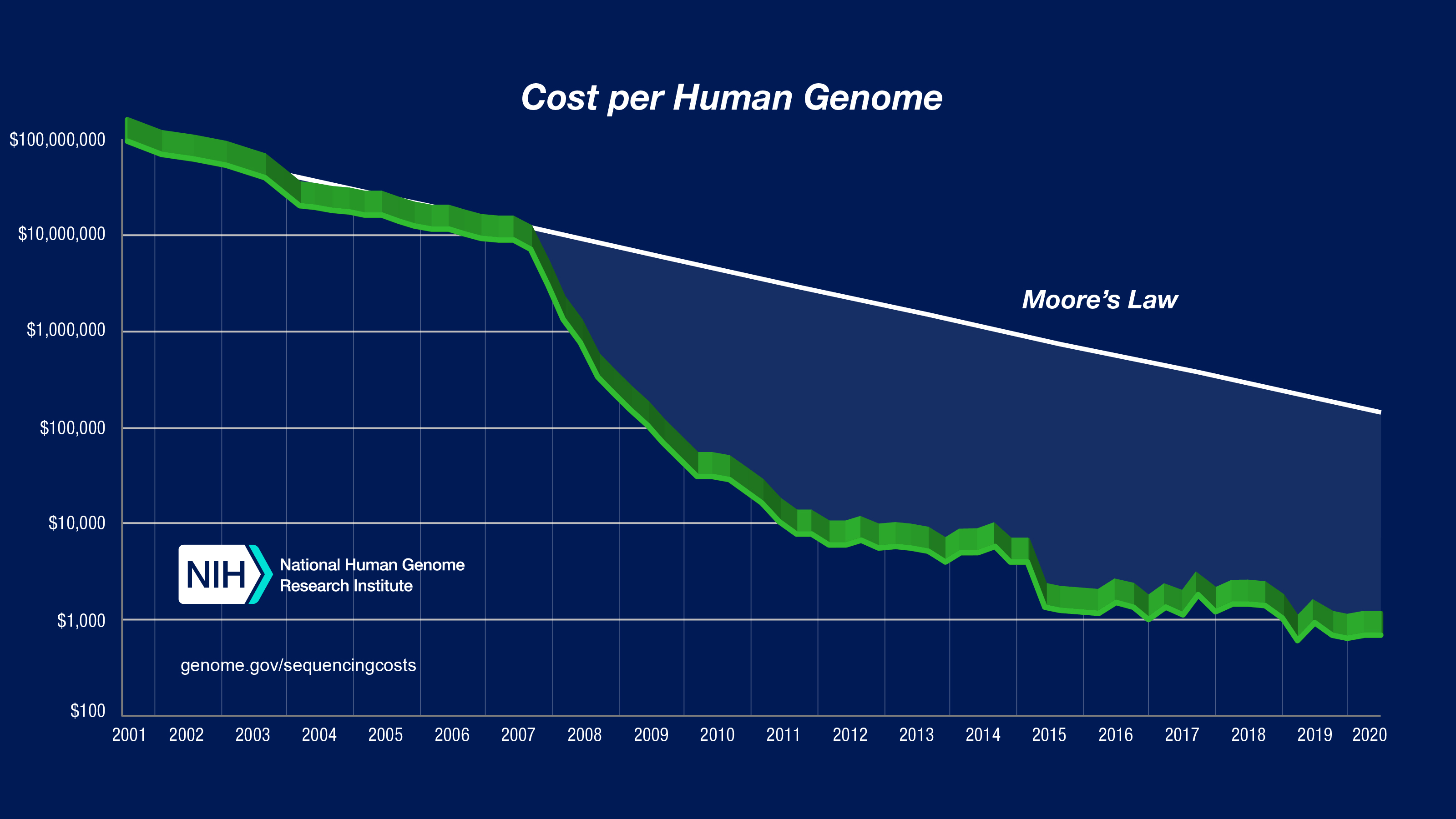
Với phương pháp đọc từng đoạn ngắn dài khoảng 150 kí tự, số lượng đoạn đọc (reads) được sinh ra vào khoảng 600 triệu.
Có 2 cách xử lý bài toán này:
Cách thứ nhất là gắn các đoạn nhỏ này theo 1 trình tự mẫu có sẵn (Sequence alignment). Trình tự mẫu có sẵn này được công bố lần đầu vào năm 2001, được xây dựng dựa trên 13 người tình nguyện tại New York, đã và đang được làm bộ gen tham chiếu cho gần như toàn bộ các nghiên cứu về hệ gen của loài người.
Cách thứ hai là lắp ráp mới hoàn toàn, không dựa theo khuôn mẫu (De novo assembly).
Tuy vậy, bộ gen tham chiếu này sẽ không phù hợp với những quần thể người tương đối khác biệt với dân Âu-Mỹ. Điều này dẫn đến các nghiên cứu đòi hỏi chính xác cao, riêng biệt cho những sắc dân Á, Phi rất khó thực hiện, cản trở sự phát triển của Y học chính xác tại các quốc gia này. Trước thách thức đó, các nước Đông Á như Nhật, Hàn, Trung đều đã xây dựng bộ gen tham chiếu riêng của mỗi nước. Để làm điều này, bắt buộc phải sử dụng các công cụ De novo assembly, đây cũng là một thách thức lớn, khi mà chương trình lắp ráp phải giải quyết các đoạn DNA lặp lại (Tandem repeat), các đoạn giống nhau trên DNA, hay các đoạn kéo dài chỉ bao gồm 1 kí tự (poly mononucleotide). Không chỉ về mặt phương pháp, cách thức cài đặt cũng hết sức quan trọng, khi chương trình cần tối ưu về bộ nhớ, số luồng, thậm chí phải sử dụng được các hệ thống tính toán phân tán để giảm thiểu thời gian tính toán.
Thuật toán lắp ráp không dựa theo khuôn mẫu
Thuật toán này giả định rằng không có thông tin nào khác ngoài những đoạn đọc được cấp. Sau đó trải qua các bước lắp ráp để tạo thành chuỗi nhiễm sắc thể.
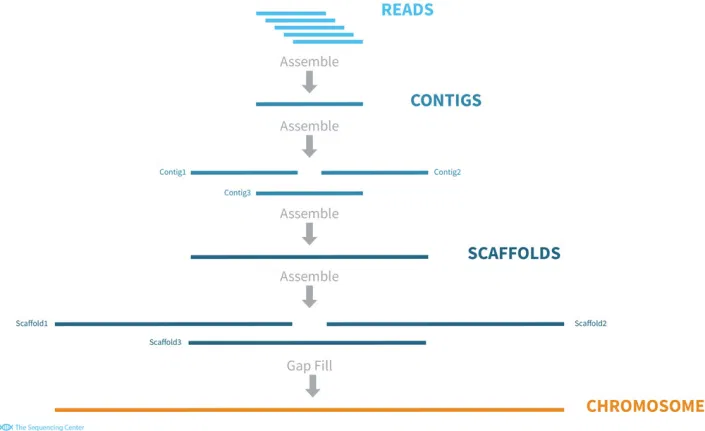
Ở mỗi bước của thuật toán, các nhà nghiên cứu đặt tên cho kết quả đầu ra để tiện cho việc theo dõi:
Đoạn liên tiếp (contigs hay contiguous) là một tập của các đoạn đọc có điểm chung với nhau.
Dải (scaffolds) là một tập của các đoạn liên tiếp được sắp sếp theo thứ tự. Dải có thể chứa đoạn trống (gap).
Ta đi sơ lược vào các bước của thuật toán:
Bước đầu tiên, một phần hoặc toàn bộ những đoạn đọc giao nhau sẽ được ghép thành một hoặc nhiều đoạn liên tiếp. Kế đến, những đoạn liên tiếp giao hoặc không giao nhau được kết hợp theo thứ tự, tạo ra một hoặc nhiều dải. Những dải này liên kết tạo ra một nhiễm sắc thể.
Với bước tạo ra đoạn liên tiếp, đoạn đọc phải chồng lên nhau một số base nhất định trước khi được nối với nhau.
Với bước tạo dải, đoạn liên tiếp không nhất thiết phải giao nhau mà có thể được liên kết bởi chuỗi bắt cặp đôi hoặc đoạn đọc dài (long reads).
Trong bước tạo thành nhiễm sắc thể, các dải được ghép lại với nhau thông qua một số quá trình phủ đoạn trống (gap-filling), co đoạn trống (gap-closing),… Bước này khá khó hoặc đôi khi không thể nếu chỉ sử dụng những đoạn đọc ngắn vì những vùng lặp ngăn cản quá trình phủ đoạn trống. Để hoàn thành việc lắp ráp nhiễm sắc thể, đôi khi nhiều công nghệ giải trình tự được sử dụng cùng lúc kèm với những giao thức lắp ráp lai (hybrid assembly protocols). Thông thường, người ta sẽ kết hợp giữa công nghệ giải trình tự đoạn đọc ngắn và đoạn đọc dài với bản đồ quang học (optical maps), bản đồ Bionano (Bionano maps). Tuy nhiên, chi phí cho việc sử dụng nhiều công nghệ sẽ khá cao.
Sau khi hoàn thành thuật toán, Quast sẽ được dùng làm thước đo đánh giá chất lượng của các dải.
Điểm mạnh của thuật toán này:
Khi sinh vật không có nhiều thông tin về gen, protein, thuật toán hoạt động tốt.
Cho phép phát hiện các cấu hình di truyền mới ví dụ sự kiện chuyển gen ngang, đảo đoạn, …
Điểm yếu của thuật toán này:
Cần nhiều tính toán.
Không tốt khi tìm kiếm sự khác biệt nhỏ ở những bộ gen thông dụng (well known genomes).
Bài viết này sẽ chỉ tập trung vào hai lớp lớn của thuật toán lắp rắp không dựa theo khuôn mẫu là OLC (Overlap-Layout-Consensus assembly) và DBG (De Bruijn graph assembly) với mong muốn cung cấp cho người đọc một góc nhìn khái quát.
Thuật toán OLC
Thuật toán này khá thuận theo trực giác tự nhiên, được phát triển đầu tiên bởi Staden vào năm 1980, sau đó được nhiều nhà khoa học khác đóng góp. OLC được phổ biến kèm theo sự thông dụng của công nghệ giải trình tự Sanger. Ngày nay, OLC được dùng bởi nhiều trình lắp ráp như Arachne, Celera Assembler, CAP3, PCAP, Phrap, Phusion, và Newbler.
Thuật toán này bao gồm 3 bước chính:
Tìm phần giao giữa từng cặp đoạn đọc để tạo đồ thị chồng chéo. (Overlap)
Bó các nhánh của đồ thị chồng chéo thành đoạn liên tiếp.
Chọn các chuỗi nu hợp lí nhất cho mỗi đoạn liên tiếp.
Tìm phần giao giữa từng cặp đoạn đọc
Bài toán này được phát biểu như sau: Cho S là tập n chuỗi có độ dài khác nhau được tạo thành từ 4 kí tự: A, T, G, C. Với mỗi chuỗi x trong tập S, tìm tất cả đoạn giao nhau với chuỗi y (khác x) sao cho tiền tố của x là hậu tố của y.
Ví dụ: cho chuỗi X là CTCTAGGCC, Y là TAGGCCCTC.
Hậu tố của chuỗi Y là tiền tố của chuỗi X: CTC.
Hậu tố của chuỗi X là tiền tố của chuỗi Y: TAGGCC.
Bài này có thể giải bằng nhiều cách.
Cách 1: Thuật toán vét cạn
Cắt lần lượt tiền tố của X, tìm hậu tố tương ứng trên Y.
Độ phức tạp trung bình: O(n^2*d^2) với d độ dài trung bình của tất cả chuỗi trong S.
Cách 2: Dùng cây hậu tố
Ta sẽ thêm 2 kí tự đặc biệt khác với các base để đánh dấu kết thúc của chuỗi X và chuỗi Y.
Chuỗi X: CTCTAGGCC#
Chuỗi Y: TAGGCCCTC$
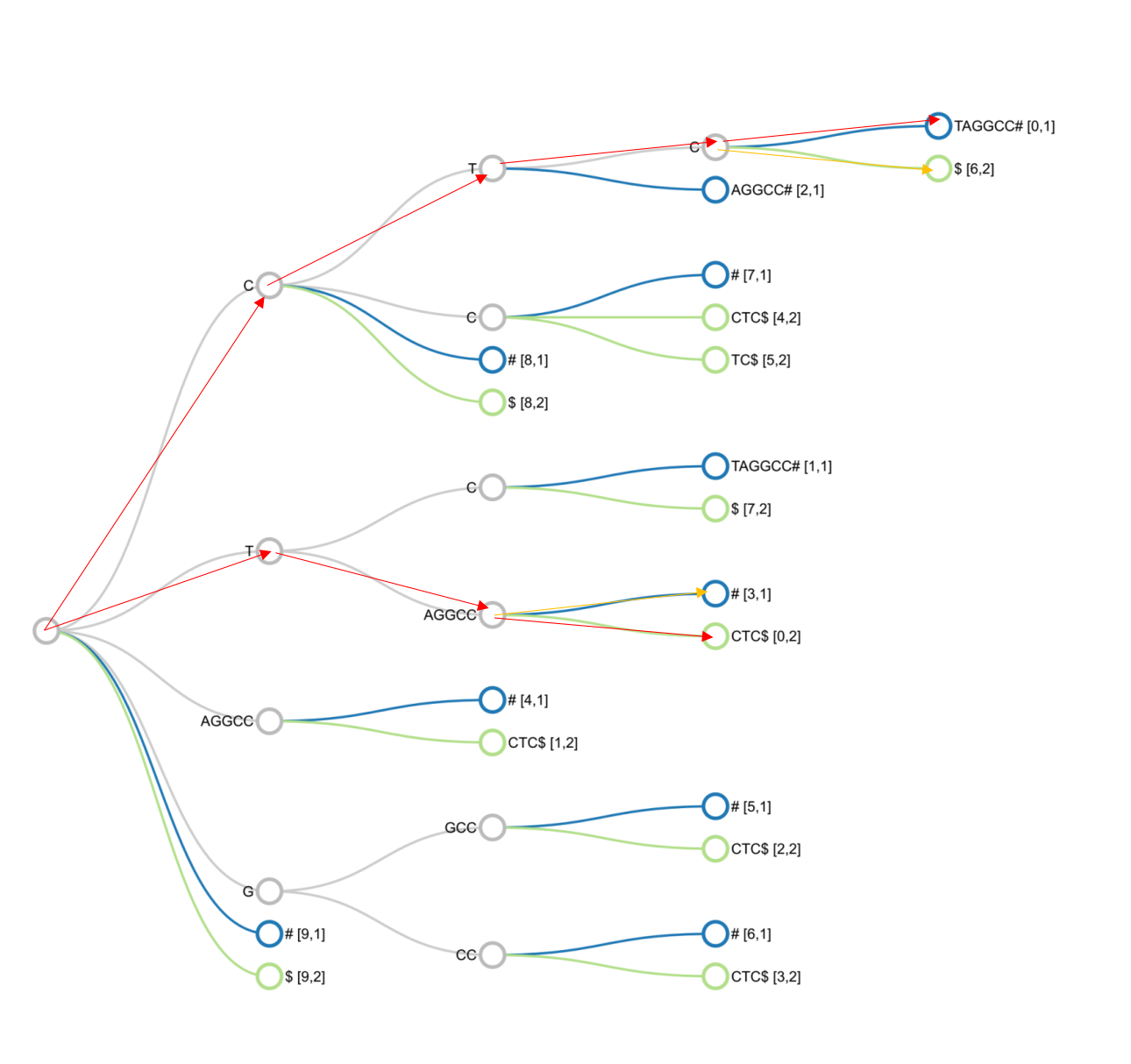
Hình trên thể hiện cây hậu tố được xây dựng từ hai chuỗi X, Y.
Với mỗi chuỗi, ta lần lượt truy vấn trên cây. Bắt đầu từ nút gốc, đi theo con đường màu đỏ, ta được chuỗi truy vấn. Cạnh nối màu cam thể hiện đoạn giao nhau giữa hai chuỗi.
Độ phức tạp cho cách giải này như sau:
Giả sử tổng độ dài của các đoạn đọc là N=n*d, a là số cặp đoạn đọc giao nhau.
Thời gian để dựng cây hậu tố là: O(N).
Tìm ra con đường màu đỏ là: O(N).
Tìm ra đoạn chồng chéo (màu cam) là: O(a). Trong trường hợp xấu nhất là O(d^2)
Độ phức tạp trung bình sẽ là O(N+a).
Cách 3: Dùng phương pháp quy hoạch động
Cách này sẽ linh hoạt hơn vì cho phép chúng ta điều chỉnh số lượng các kí tự không khớp nhau để có được đoạn giao nhau lớn hơn. Ví dụ:
X: CTCGGCCCTAGG
| | | | | | | |
Y: GGCTCTAGGCCC
Áp dụng hàm tính điểm và công thức truy hồi như trong hình sau:
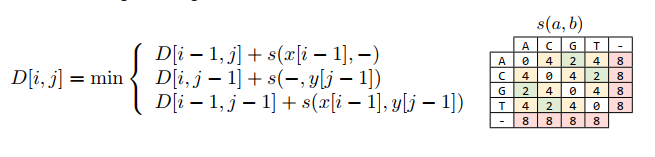
Kết quả thu được ma trận sau:
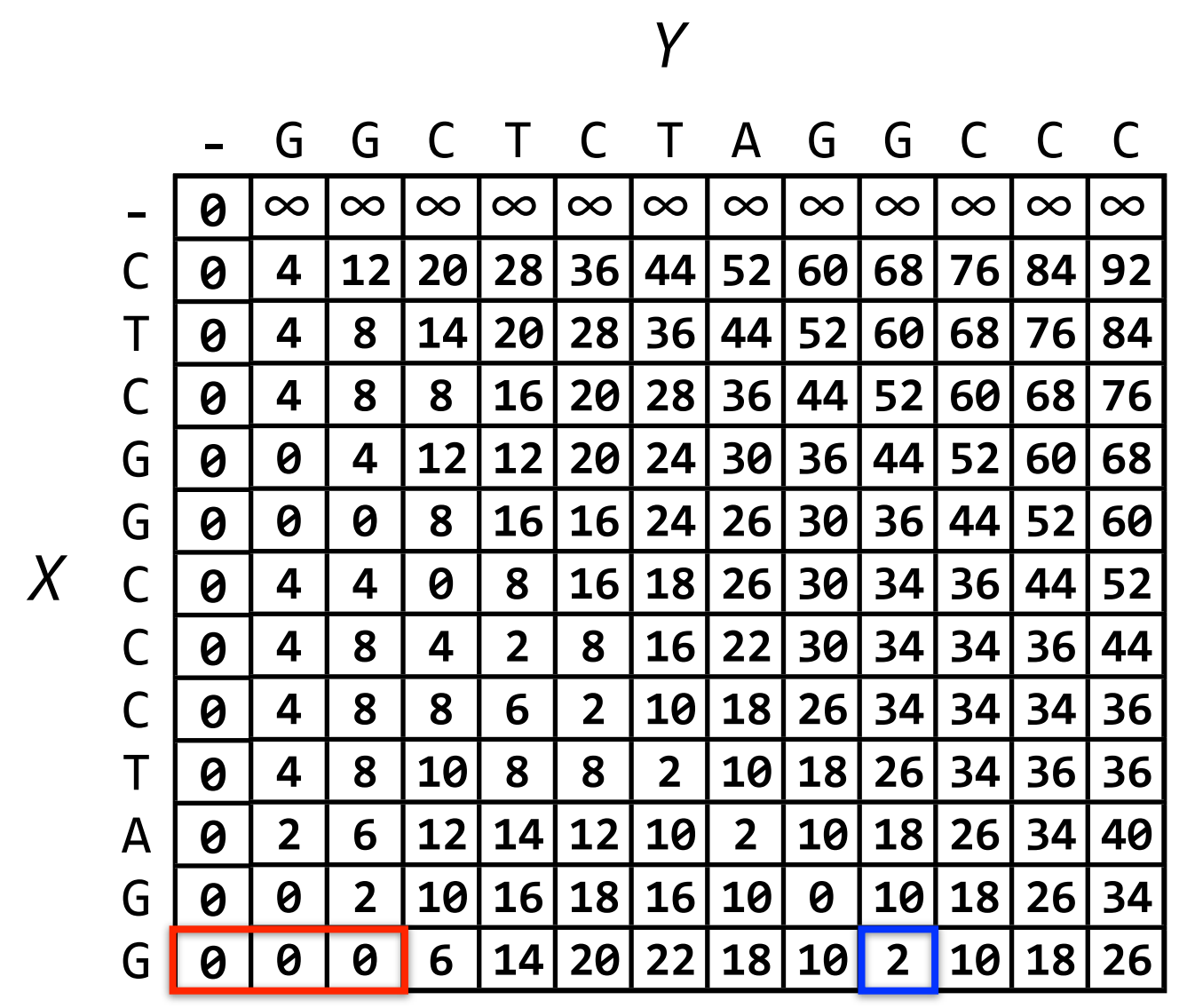
Truy ngược từ dòng cuối cùng, ta chọn ô có giá trị thấp nhất rồi lần ngược theo công thức truy hồi. Nếu chọn ô có giá trị thấp nhất (giá trị 0) sẽ thu được GG trong khi ta đang muốn thu được đoạn giao nhau GGCTCTAGG (kết thúc ở ô viền xanh). Vậy nên, để có thể thu được đoạn giao nhau có độ dài lớn hơn, ta cần khởi tạo mảng với giá trị lớn vô cùng cho các ô đầu tiên ở dòng cuối cùng. Ví dụ, ta chọn độ dài đoạn giao nhau không nhỏ hơn 5, ta thu được kết quả như hình bên dưới:
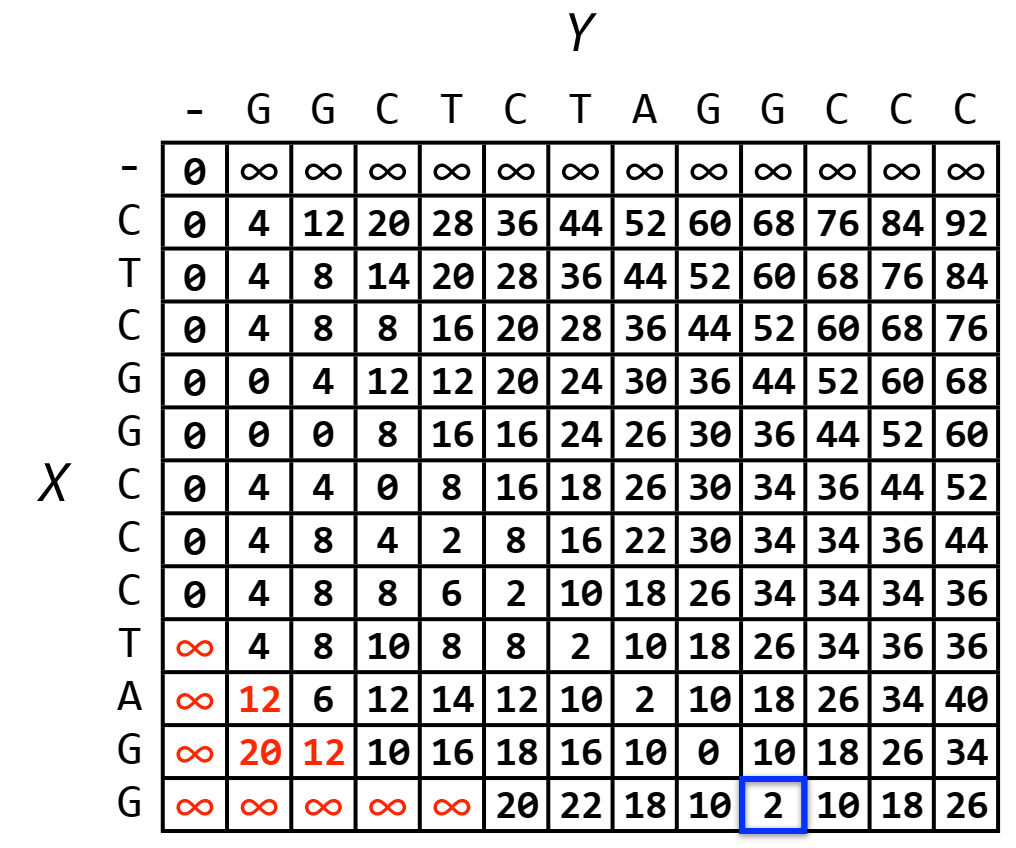
Độ phức tạp của cách này như sau:
Số lượng cặp cần tính ma trận: O(n^2)
Kích thước ma trận quy hoạch động: O(d^2)
Độ phức tạp trung bình: O(n^2*d^2) = O(N^2).
Trong thực tế, cách 2 và cách 3 được dùng phối hợp với nhau. Cách 2 được dùng để lọc ra những cặp giao nhau, rồi cách 3 được dùng để tìm đoạn giao nhau theo các điều kiện.
Trong cả thuật toán lắp ráp, việc tìm giao nhau giữa từng cặp chuỗi tốn nhiều thời gian nhất. Vậy nên có nhiều phương pháp ngoài 3 cách được đề xuất để tiết kiệm thời gian tính toán ở bước này ví dụ như so khớp chuỗi gần đúng (approximate string matching), …
Bó các nhánh của đồ thị chồng chéo thành đoạn liên tiếp
Giả sử ta làm việc với một chuỗi như sau: to_every_thing_turn_turn_turn_there_is_a_season với độ dài đoạn giao nhau là 4, cắt thành mỗi đoạn có độ dài là 7.
Đồ thị chồng chéo là một đồ thị có hướng với mỗi nút là một chuỗi, cung có hướng từ chuỗi có hậu tố tới chuỗi có tiền tố giống nhau. Từ chuỗi ví dụ, đồ thị chồng chéo xây dựng được như hình sau:
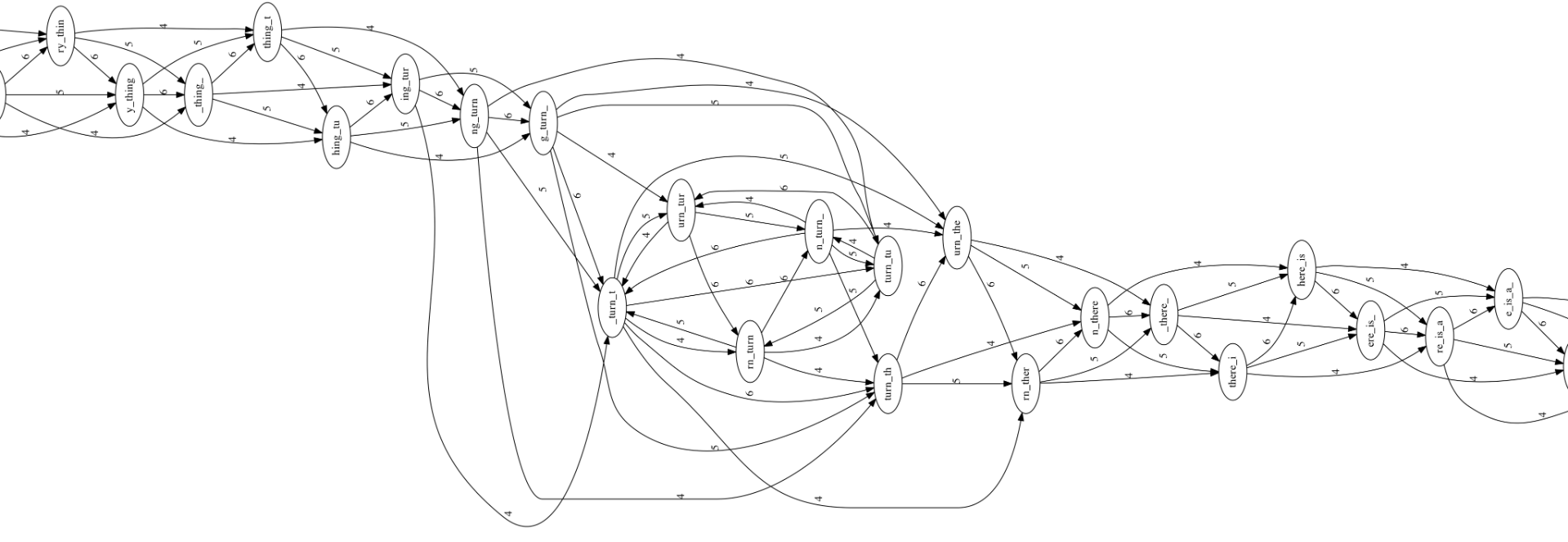
Đồ thị này lớn và phức tạp. Các đoạn liên tiếp cũng không dễ dàng thấy. Ta sẽ chọn 1 phần đồ thị để xem xét kỹ hơn.
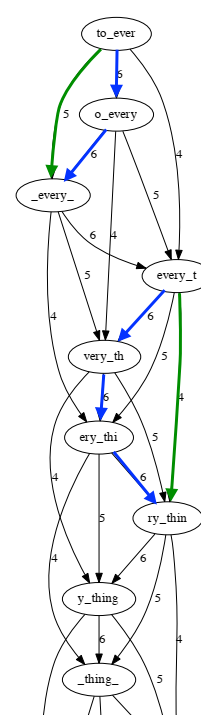
Các cạnh màu lục có thể suy ra từ các cạnh màu lam nên các cạnh màu lục cần được loại bỏ khỏi đồ thị để làm đồ thị đơn giản hơn.
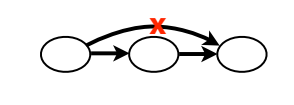
Bắt đầu với xóa các cạch vượt qua 1 nút. Ta thu được đồ thị như hình:

Ta tiếp tục thực hiện xóa các cạnh nhảy quả 2 nút.
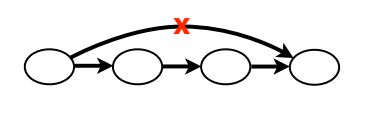
Kết quả thu được một đồ thị chồng chéo đơn giản hơn ban đầu rất nhiều.

Từ đồ thị này, ta dễ dàng nhìn thấy 2 đoạn liên tiếp rõ ràng, và 1 vùng lặp.

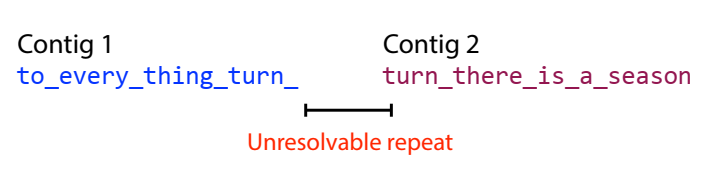
Trong thực tế, bước bó các nhánh của đồ thị thành đoạn liên tiếp cũng xử lý đồ thị con “giả” (spurious subgraphs) gây ra bởi lỗi trong quá trình giải trình tự. Ví dụ:
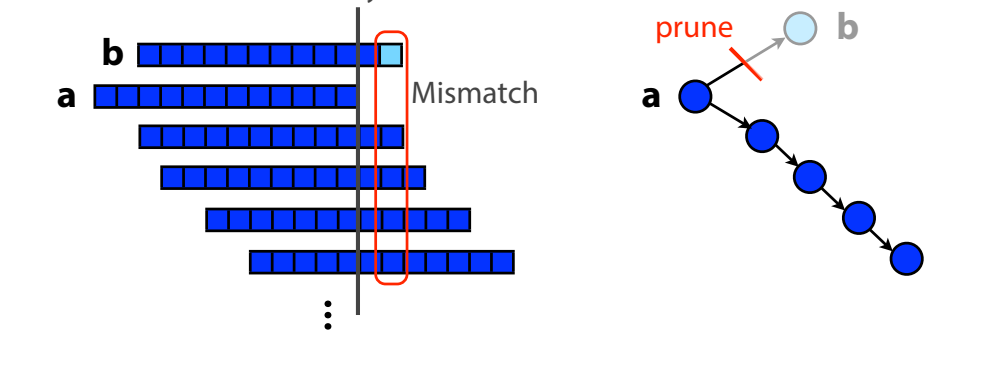
Đoạn đọc b bị sai khác so với các đoạn đọc khác ở base cuối cùng do quá trình giải trình tự bị lỗi. Khi tạo ra đồ thị chồng chéo, lỗi này sẽ tạo ra một nhánh cụt đi từ a tới b. Dựa vào đồ thị, ta có thể loại bỏ đoạn đọc này.
Chọn các chuỗi nu hợp lí nhất cho mỗi đoạn liên tiếp
Sau khi tìm ra được các đoạn liên tiếp từ đồ thị, các đoạn đọc tạo nên từng đoạn liên tiếp được gióng thành từng hàng, rồi lựa chọn nu cho từng vị trí vì có thể có sai khác ở vài đoạn đọc trên cùng một vị trí. Sự sai khác này có thể gây ra bởi lỗi quá trình giải trình tự hoặc do bội thể (ploidy). Thông thường, nu được chọn là nu xuất hiện trên nhiều đoạn đọc nhất.

Thuật toán OLC sử dụng đồ thị chồng chéo để tạo các đoạn liên tiếp tương ứng với bài toán tìm đường đi Hamilton hoặc chu trình Hamilton. Bài toán này thuộc lớp NP và là NP-hard. Hiện nay, vẫn chưa có giải thuật hiệu quả để tìm đường đi Hamilton.
Thuật toán DBG
DBG là một thuật toán phản trực giác, được giới thiệu chính thức vào năm 1995 bởi Ramana M. Idury và Michael S. Waterman. Phần mềm lắp ráp chuyên dụng đầu tiên sử dụng thuật toán này là EULER, được phát hành vào năm 2001 bởi Pavel Pevzner và Michael Waterman. Ban đầu, DBG không được biết đến trong thời gian dài. Tuy nhiên, nhờ vào công nghệ giải trình tự của Illumina thâm nhập thị trường, một vài trình lắp ráp được phát triển dựa trên nó đã ra đời như Euler-USR, Velvet, ABySS, AllPath-LG, SOAPdenovo, ABySS 2.0,… Các trình này bước đầu thành công trên một số bộ gen nhỏ như vi khuẩn, sau đó mở rộng dần ra dưa chuột, gấu trúc. Từ đó, các nhà nghiên cứu khắp thế giới có một phương pháp tiết kiệm chi phí mới để tạo ra bản nháp của bộ gen lớn.
Thuật toán này có 2 bước:
Tạo k-mer từ các đoạn đọc
Xây dựng đồ thị De Bruijn.
Tạo k-mer
k-mer là một chuỗi con có độ dài là k. Ví dụ chuỗi S là GGCGA, 3-mer của S là GGC, GCG, CGA.
Xây dựng đồ thị De Bruijn
Giả sử ta có các 3-mer từ chuỗi AAABBBA như sau: AAA, AAB, ABB, BBB, BBA. Ta sẽ tạo các k-1-mer trái (L) và phải (R). Từ AAB, k-1-mer trái là AA, k-1-mer phải là AB.
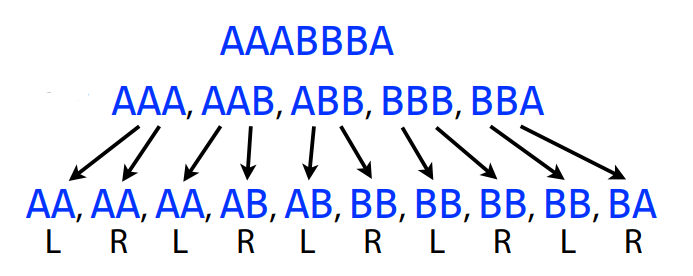
Trong đồ thị De Buijn, mỗi nút là k-1-mer, cung có hướng từ k-1-mer trái tới k-1-mer phải và biểu diễn cho đoạn chồng chéo giữa hai k-1-mer.

Nếu thêm một B vào chuỗi ví dụ: AAABBBBA, đồ thị De Bruijn mới sẽ có đa khuyên:
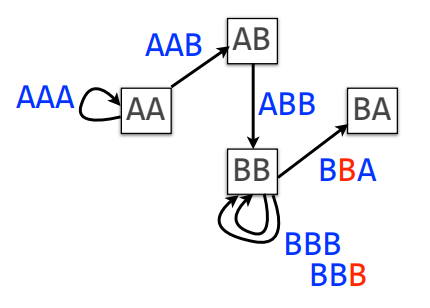
Từ ví dụ này, đồ thị De Bruijn là một đa đồ thị. Dễ thấy, để dựng một bộ gen, ta cần phải đi qua mỗi cung đúng một lần. Trong lý thuyết đồ thị, đây là bài toán tìm đường đi hoặc chu trình Euler. Một tính chất quan trọng của đồ thị Euler (có đường đi hoặc chu trình Euler) là không có hoặc có đúng 2 đỉnh bán cân bằng, các đỉnh còn lại cân bằng. Với một chuỗi hoàn hảo (không phải là chuỗi vòng) thì luôn tạo được một đồ thị Euler vì tồn tại duy nhất hai đỉnh bán cân bằng: một là đỉnh tạo bởi k-1-mer trái cùng, hai là đỉnh tạo bởi k-1-mer phải cùng, các đỉnh còn lại đều cân bằng.
Trong thực tế, bộ gen có rất nhiều vùng lặp vậy nên có thể có nhiều đường đi hoặc chu trình Euler trên đồ thị De Bruijn. Ví dụ: cho chuỗi ZABCDABEFABY, k=3 (k-mer), ta xây dựng được đồ thị như hình sau:
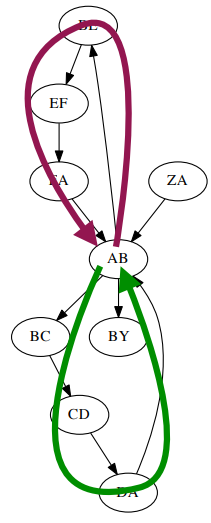
Các đường đi Euler có thể là:

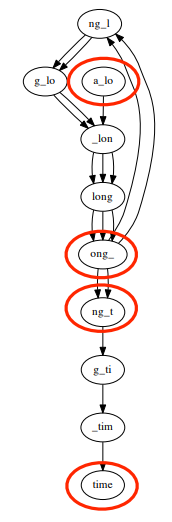
Đối với một chuỗi có nhiều đoạn lặp lại, vấn đề về khác biệt giữa độ phủ dẫn tới đồ thị không liên thông và không phải đồ thị Euler. Ví dụ đồ thị De Brujin cho chuỗi a_long_long_long_time, k = 5 (5-mer), từng thành phần thì liên thông như đồ thị thì không liên thông, đồ thị có 4 đỉnh bán cân bằng.
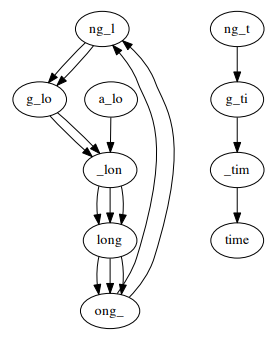
Bên cạnh đó, lỗi và sự khác biệt giữa các nhiễm sắc thể có thể dẫn tới đồ thị không Euler và không liên thông. Vì dụ a_long_long_long_time, k = 5 với 1 đoạn lỗi từ long_ thành lxng_.
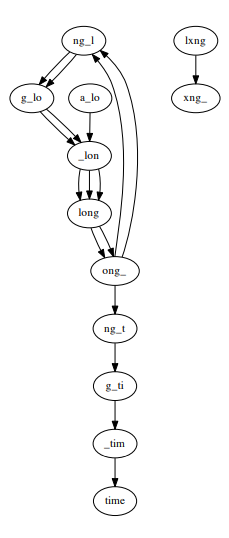
Tuy gặp các vấn đề độ phủ không đồng nhất, lỗi trong quá trình giải trình tự, nhiều chu trình hoặc đường đi Euler, độ phức tạp thời gian dựng lên đồ thị De Bruijn là O(N) và độ phức tạp không gian O(min(G,N)) (length of genome is G).
So sánh hai lớp thuật toán
Cả hai lớp thuật toán giải quyết những vùng lặp trên gen bằng cách chia thành từng đoạn liên tục.
OLC có điểm yếu:
Dựng đồ thị chồng chéo tốn khá nhiều thời gian. Độ phức tạp rơi vào O(N+a) hoặc O(N^2).
Đồ thị chồng chéo lớn; một nút tương ứng với một đoạn đọc; số lượng cạnh tăng lên theo cấp siêu tuyến tính (superlinear) với số lượng đoạn đọc. Trong khi đó, với công nghệ giải trình tự thế hệ mới (next generation sequencing), tập dữ liệu có thể chứa tới hàng trăm triệu hoặc hàng tỷ đoạn đọc với hàng trăm tỷ nu.
DBG có điểm yếu:
Vì các đoạn đọc được chưa thành k-mers nên việc giải quyết các vùng lặp không tốt bằng OLC.
Chỉ có một vài loại giao nhau được quan tâm nên tạo ra sự khó khăn với việc giải quyết lỗi.
Tính mạch lạc của đoạn đọc bị mất. Một vài đường đi trên đồ thị không thống nhất với các đoạn đọc.
Phải xử lý các đoạn đọc lỗi trước khi xây dựng đồ thị.
Có nhiều đường đi hoặc chu trình Euler có thể có.
Điểm vượt trội của DBG so với OLC là độ phức tạp không gian O(min(G,N)).
Tạm kết
Bài viết này cố gắng đưa một cái nhìn đủ sâu về hai lớp lớn thuật toán lắp ráp không dựa theo khuôn mẫu. Mỗi lớp có điểm mạnh, điểm yếu riêng. Trong thực tế, các nhà nghiên cứu thường dùng song song hai lớp này tùy vào nhu cầu, mục đích, tài nguyên có sẵn để khảo sát, so sánh và chọn cho hướng đi cho dự án. Có khá nhiều trình lắp ráp sử dụng hai lớp thuật toán lắp ráp trên. Mỗi trình lại có các cài đặt riêng, cải tiến riêng để giúp giải quyết các vấn đề tồn đọng như lỗi của quá trình giải trình tự, bội thể hoặc thời gian tính toán lớn, bộ nhớ lớn, … Ngoài ra, các thuật toán khác vẫn đang được nghiên cứu và phát triển với mục tiêu lắp ráp bộ gen nhanh hơn, chính xác hơn. Đây thực sự là một mảnh đất tiềm năng cho các bạn yêu mến thuật toán thử sức, vừa thỏa mãn đam mê vừa đóng góp vào sự phát triển của ngành tin sinh học.
Trong khuôn khổ dự án 1000 hệ gen người Việt Nam, Vinbigdata đã thu hút được những tài năng về công nghệ thông tin, điển hình là anh Trần Quang Khải – người từng đoạt huy chương vàng IOI, để xây dựng một phần mềm tối ưu lắp ráp hệ gen người Việt với yêu cầu vừa cải thiện được tốc độ so với các phần mềm khác, vừa sử dụng bộ nhớ tối ưu.
Nguồn tham khảo
Lecture OCL Assembly – Johns Hopkins University